Обращаете ли вы внимание, если крыша дома и палатка почти одинаковой формы? Если вы посмотрите еще раз, похоже, что он состоит из двух треугольников на каждом конце, затем покрытых одеялом прямоугольной формы. Эта форма также известна как треугольная призма. Называется он так потому, что основание и крышка треугольные. В геометрии мы изучим определение и формулу треугольных призм. По этому поводу мы также обсудим различные примеры проблемы, чтобы лучше понять этот материал.
Призма - это форма, которая имеет крышку и основание с конгруэнтной n-сторонней формой, а вертикальные стороны имеют прямоугольную форму.
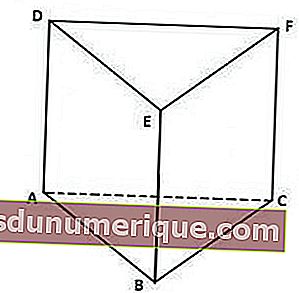
Треугольные призмы обладают следующими характеристиками:
Имеет конгруэнтное треугольное основание и крышку.
На изображении выше крышка призмы, а именно треугольник DEF, имеет ту же форму и размер, что и треугольник ABC в качестве его основания.
Прямоугольник как вертикальная сторона.
Вы можете видеть, что призма выше ограничена тремя прямоугольниками с каждой стороны вертикали, а именно прямоугольниками ACFD, BCFE и ABED.
Имеет 5 сторон, 9 ребер и 6 вершин.
5 сторон треугольной призмы состоят из 1 стороны основания, 1 стороны крышки и 3 сторон вертикали. В то время как 9 ребер состоят из 3 вертикальных ребер, 3 сторон основания и 3 сторон крышки. Кроме того, 6 вершин - это точки A, B, C, D, E и F.
Теперь, когда мы знаем характеристики, а также значение треугольной призмы, пришло время познакомиться с формулами треугольной призмы и примерами их проблем.
Формулы треугольной призмы и примеры задач
Мы изучим два вида формул треугольной призмы. Формула для определения объема и формула для определения площади поверхности. Формулы такие:
Объем
Для объема воспользуемся формулой:
V = площадь основания × высота
или
V = (½ x a x h) × высота призмы
Итак, чтобы лучше понять это, давайте рассмотрим пример этой проблемы:
Высота призмы 10 см. Основание призмы имеет форму прямоугольного треугольника со сторонами 4 см и 3 см соответственно. Каков объем этой треугольной призмы?
Решение:
Здесь нам просто нужно подставить известные числа в такую формулу:
V = (½ x a x h) × высота призмы
V = (½ х 4 х 3) × 10
V = 6 × 10
V = 60 см 3
Площадь поверхности
При расчете площади поверхности треугольной призмы мы будем использовать следующую формулу:
L = (2 x площадь основания) + (площадь всех перпендикулярных сторон)
если треугольник равносторонний, то можно воспользоваться формулой:
L = (2 x площадь основания) + (3 x площадь одной стороны от вертикали)
Или это может быть формула:
L = (2 x площадь основания) + (периметр основания x высота призмы)
Давайте рассмотрим пример этой проблемы, чтобы увидеть, как применяется эта формула. Вот пример проблемы:
Существует равносторонняя треугольная призма высотой 12 см, длиной стороны 5 см и высотой 8 см. Тогда какова площадь поверхности этой треугольной призмы?
Решение:
Чтобы найти площадь поверхности, мы просто используем формулу площади поверхности треугольной призмы, например:
L = (2 x площадь основания) + (3 x площадь одной вертикальной плоскости)
L = (2 х (½ х 5 х 8)) + (3 х (12 х 5))
L = 40 + 180
L = 220 см 2
Итак, это различные формулы треугольной призмы, которые вам следует знать, а также некоторые примеры проблем. Если вы все еще не уверены, спросите в столбце комментариев или попробуйте Smart Class, надежную платформу онлайн-обучения в мире.