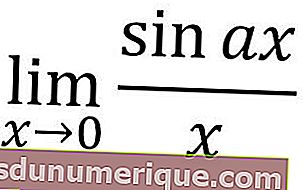Предел триггерной функции определяется как ближайшее значение к углу в триггерной функции. Это вычисление можно заменить как предел алгебраической функции, но с тригонометрической функцией, которую необходимо изменить в первую очередь.
Тригонометрическая функция должна быть преобразована в тригонометрическое тождество для неопределенного предела, который представляет собой предел, который, если его подставить, будет равен 0. Кроме того, существует также способ вычислить неопределенный предел без использования тригонометрического тождества, но с использованием тригонометрической предельной теоремы. Другие используют и тождество, и теорему одновременно.
Для определения предельного значения тригонометрических функций можно использовать различные способы, а именно численные методы, подстановку, разложение на множители, время равноправия и производные.
(Также прочтите: Измерение видимости с помощью тригонометрических формул)
Но исходя из значения, мы можем разделить эту формулу на две, то есть те, которые близки к числу и близки к нулю.
X приближение к числу
Если у нас есть предел тригонометрической функции, x которой приближается к числу c, мы можем определить его значение, подставив c в тригонометрическую функцию. Формулы следующие.

X приближается к нулю
Если x предела тригонометрической функции приближается к нулю, мы можем использовать следующие формулы.

Если после подстановки значения x в тригонометрическую функцию неопределенная форма равна 0/0 ∞ / ∞, то для определения предельного значения тригонометрической функции можно использовать правило Л'Оспиталя, а именно
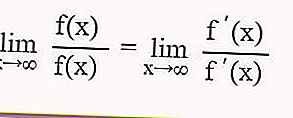
Интуиционное понимание пределов триггерных функций
Интуитивно понять предел тригонометрической функции - то же самое, что и предел алгебраической функции. Предел триггерной функции существует тогда и только тогда, когда существуют левый предел и правый предел, а левый предел равен правому пределу.