Вы когда-нибудь видели движение маятника или пружины? Два движения, которые вы наблюдаете, классифицируются как простые гармонические движения. Это движение вперед и назад вокруг точки баланса. Если вы обратите внимание, маятник имеет точку равновесия посередине, потому что, даже если его скорость уменьшается, маятник все равно будет двигаться вокруг точки равновесия.
Простое гармоническое движение имеет фиксированную амплитуду (максимальное отклонение) и частоту. Это движение периодическое. Каждое движение будет происходить неоднократно и регулярно в один и тот же временной интервал.
В простом гармоническом движении результирующая сила имеет то же направление, а именно к точке равновесия. Эта сила называется возвращающей силой. Величина восстанавливающей силы прямо пропорциональна положению объекта в точке равновесия.
Некоторые из характеристик этого движения включают график положения частицы как функции времени в форме синуса или косинуса. Это движение также можно увидеть из уравнения отклонения, уравнения скорости, уравнения скорости и уравнения энергии движения.
(Также читайте: Величины в концепции прямого движения)
Основываясь на этих характеристиках, простое гармоническое движение имеет отклонение, скорость, ускорение и энергию.
Отклонение
Простое гармоническое отклонение можно представить как проекцию частиц, движущихся по правильным кругам, на диаметр круга. В целом уравнение отклонения в этом движении выглядит следующим образом.
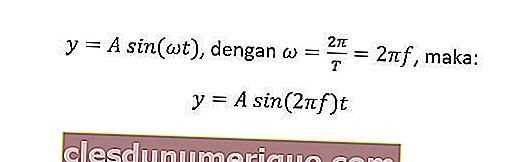
y = отклонение колебаний (м)
ω = угловая скорость (рад / с)
T = период (с)
f = частота (Гц)
t = время в пути (с)
A = максимальная амплитуда / отклонение (м)
Скорость
Скорость - это первая производная от позиции. В простом гармоническом движении скорость получается из первой производной уравнения отклонения. Уравнение скорости можно описать следующим образом.

Ускорение
Ускорение простого гармонического движущегося объекта может быть получено из первой производной уравнения скорости или второй производной уравнения отклонения. Уравнение ускорения можно получить следующим образом.
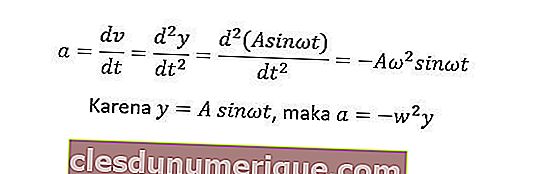
Максимальное отклонение имеет значение, равное амплитуде (y = A), поэтому максимальное ускорение am = - Aw
Энергия
Уравнение энергии в простом гармоническом движении включает кинетическую энергию, потенциальную энергию и механическую энергию. Кинетическую энергию объекта можно сформулировать следующим образом.
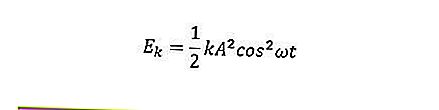
Потенциальную энергию объекта можно сформулировать следующим образом.
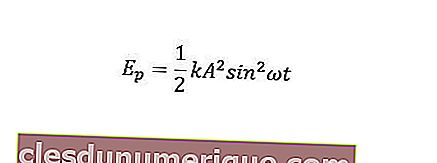
Между тем механическая энергия - это сумма кинетической энергии и потенциальной энергии.
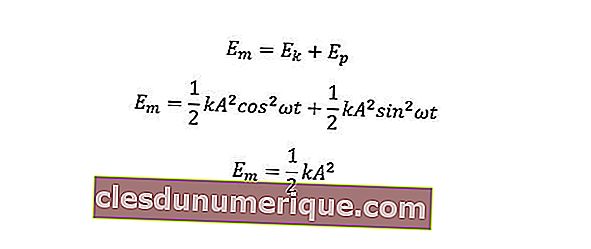
k = фиксированное значение (Н / м)
ω = угловая скорость (рад / с)
A = амплитуда (м)
t = время в пути (с)
Количество потенциальной энергии и кинетической энергии объекта, движущегося по простым гармоникам, всегда фиксировано.









