Если вы изучаете математику, вы, должно быть, слышали или изучали тригонометрию. Ну, тригонометрия - это раздел математики, изучающий взаимосвязь между углами и длинами сторон треугольников, например, такими как синус, косинус и тангенс. Буквально тригонометрия происходит от греческого языка: trigonon, что означает «три угла», и metron, что означает «измерять». Как и в случае с различными материалами по математике, есть тригонометрические формулы, которые вам необходимо знать.
По этому поводу мы постараемся разобраться в различных формулах, а также на примерах их проблем.
Тригонометрические формулы
Понятие тригонометрии - важное понятие в треугольниках. Тригонометрические значения формулируются на основе отношения длин сторон прямоугольного треугольника. Существует шесть значений тригонометрического отношения, а именно синус (sin), косинус (cos), тангенс (tan), косеканс (косеканс), секанс (секунды) и котангенс (cot). Шесть типов тригонометрических значений можно определить путем сравнения длин сторон по определенным правилам.
Тригонометрия используется во многих сферах, начиная от астрономии, географии, теории музыки, акустики, оптического анализа финансового рынка, электроники, теории вероятностей, статистики, биологии, медицинской визуализации, фармацевтики, химии и многих других.
А теперь настало время познакомиться с различными тригонометрическими формулами этого урока.
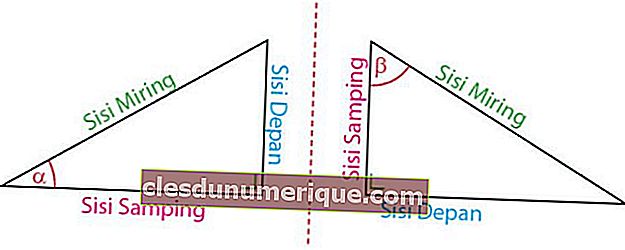
Источник изображения: idschool.net
В зависимости от расположения к углу стороны треугольника - колена делятся на три типа: передняя сторона, боковая сторона и гипотенуза. Лицевая сторона - это сторона, обращенная к углу. Сторона находится сбоку от угла. Наклонная сторона всегда находится перед углом 90o.
Итак, три основных тригонометрических функции - это функции sin, cos и tan. Определение трех функций на основе сторон и углов прямоугольного треугольника можно увидеть на рисунке и уравнении ниже.
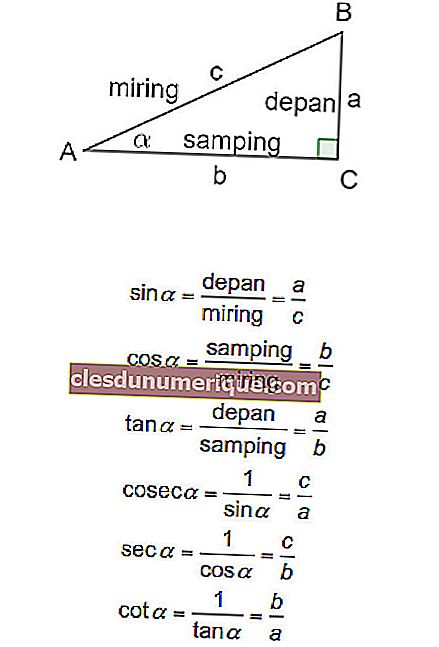
Теперь, специально для особых углов, тригонометрические значения следующие:
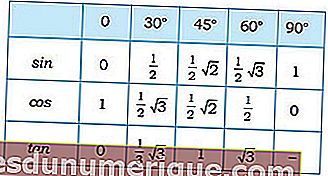
Источник изображения: madematics.net
Тригонометрическое сравнение коррелированных углов
Тригонометрическое соотношение соответствующего угла - это расширение основного тригонометрического значения, которое определяется из угла прямоугольного треугольника. Угол прямоугольного треугольника расположен только в квадранте I, потому что это острый угол, размер которого составляет 0 ° - 90 °.
Центральный угол круга составляет от 0 ° до 360 °. Угол разделен на 4 квадранта, каждый квадрант имеет диапазон 90 °.
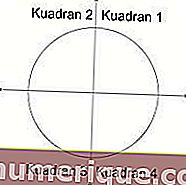
Источник изображения: studiobelajar.com
- Квадрант 1 имеет угол от 0 ° до 90 °. Все значения тригонометрических соотношений в этом квадранте положительны.
- Квадрант 2 имеет угол от 90 ° до 180 °. В этом квадранте положительны только значения синуса и косеканса.
- Квадрант 3 имеет угол от 180 ° до 270 °. В этом квадранте положительны только касательные и котангенсы.
- Квадрант 4 имеет угол 270 ° - 360 °. В этом квадранте положительны только косинус и секанс.
Тригонометрическая идентичность
Теорема Пифагора, а именно a2 + b2 = c2, является основой для подготовки тригонометрических тождеств. Тригонометрические тождества выражают отношение одной тригонометрической функции к другим тригонометрическим функциям.
Сумма квадрата синуса и квадрата косинуса равна единице. Если обе стороны разделены на квадрат косинуса, один плюс квадрат тангенса равняется квадрату секанса. Аналогичным образом, если две стороны разделены квадратом синуса, одна плюс квадрат котангенса равняется квадрату косеканы.
Вот формула идентичности:
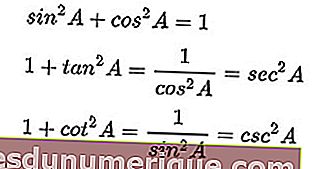
Источник изображения: wikipedia.org
Различные другие формулы
Вам следует знать еще одну формулу, а именно:
Формула суммы и разности углов:
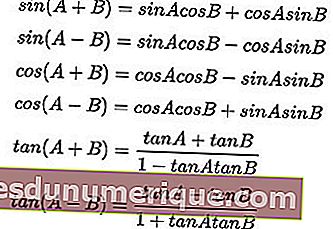
Формулы умножения триггеров:
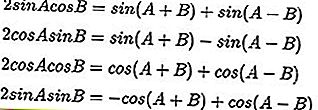
Формулы тригонометрической суммы и разности:
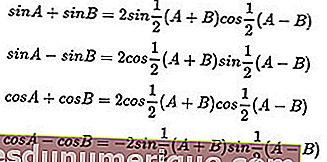
Примеры триггерных проблем
Найдите значение 2 cos 75 ° cos 15 °:
Решение:
Основываясь на информации в задаче, мы можем видеть, что указанная выше задача включает тригонометрическое умножение. Используйте формулу умножения для cos, описанную выше, которая равна 2 cos A cos B = cos (A + B) + cos (A - B).
Ответ:
2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75-15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½
Это набор формул и тригонометрических задач, которые вы можете изучить и понять. Чтобы лучше понять это, вы можете попробовать ПРОБЛЕМУ, взвешенное, полное онлайн-решение для отработки вопросов в соответствии с последней учебной программой в Smart Class. Начиная с начальной, средней и средней школы с различными предметами, такими как математика, физика, химия и другие. Здесь вы можете изучить различные виды формул с примерами задач,
Давай, чего ты ждешь! Попробуем ПРОБЛЕМНЫЕ упражнения в Smart Class прямо сейчас.





