В математике числовой узор - это комбинация нескольких чисел, образующих определенный узор. Несколько типов числовых шаблонов включают четные, нечетные, арифметические и геометрические шаблоны. Сегодня мы собираемся обсудить два типа рисунков чисел, а именно геометрические линии и геометрические ряды.
Геометрическая линия - это последовательность чисел, составленная из членов с фиксированными пропорциями. Первый член геометрической последовательности обозначается а. Отношение или сравнение между двумя терминами обозначается r.
Линии геометрии можно сформулировать следующим образом.
а, ар, ар2, ар3,…, арн-
a = первый член геометрической последовательности
r = соотношение между членами
n = последовательность терминов
Чтобы определить значение n-го члена или отношения, мы можем использовать следующую формулу.
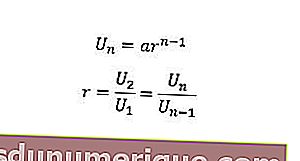
U n = n -й член
Давайте поработаем над примером проблемы ниже.
Дана геометрическая последовательность 3, 9, 27, 81, 243. Исходя из этого, затем определите соотношение геометрической последовательности!
Мы знаем U 1 = 3 и U 2 = 9, поэтому, если мы подставим их в формулу, мы получим следующий результат.
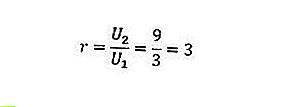
Итак, соотношение геометрической последовательности, приведенной выше, равно 3.
(Также прочтите: Математическая логика, от отрицания к биимпликации)
Между тем, геометрический ряд - это сумма членов геометрической последовательности. Геометрический ряд можно обозначить как S n, что означает количество первых n элементов геометрической последовательности.
Геометрический ряд можно сформулировать следующим образом.

a = первый член геометрической последовательности
r = соотношение между членами
n = последовательность последнего добавленного члена
U n = n -й член
Давайте поработаем над примером проблемы ниже.
Учитывая, что геометрический ряд с первым членом - 6, а четвертым - 48, тогда сумма первых шести членов будет…?
Мы знаем, что a = 6 и U 4 = 48. Если мы подставим формулу, результат будет следующим.
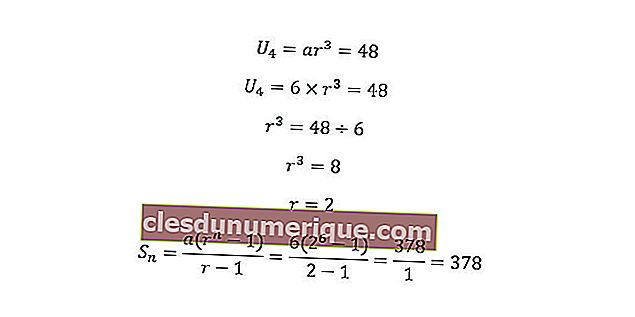
Итак, сумма первых 6 членов в приведенном выше ряду равна 378.





