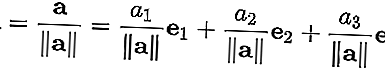Вектор в математике и физике можно определить как геометрические объекты, которые имеют величину и направление. Вектор изображен стрелкой, где основание стрелки показывает точку захвата (начальную точку) вектора, длина стрелки указывает размер или значение вектора (чем длиннее стрелка, тем больше значение или значение вектора, и наоборот) , а стрелка указывает направление вектора.
В письменном виде, если вектор начинается в точке A и заканчивается в точке B, то его можно записать маленькой буквой, над которой есть линия / стрелка вроде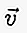 
или 
или 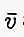также:
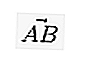
Типы векторов
Вектор в математике делится на 4 типа, в том числе:
Вектор положения
Вектор, начальная точка которого находится в 0 (0,0), а его конец - A (a1, a2).
Нулевой вектор
«Нулевой вектор» ( нулевой вектор или нулевой вектор ) - это вектор, длина которого равна «нулю». Запись в координатах этого вектора - (0,0,0), и обычно обозначается символом 
или 0 . Этот вектор отличается от других векторов тем, что он не может быть нормализован (то есть ни один единичный вектор не является кратным нулевому вектору). Сумма нулевых векторов с любым вектором a равна a (то есть 0 + a = a ).
У нулевого вектора нет четкого направления вектора.
Единичный вектор
- вектор длины «единица». Обычно единичные векторы используются только для обозначения направлений. Вектор любой длины можно разделить на длину, чтобы получить единичный вектор. Это называется «нормализацией» вектора. Единичный вектор часто обозначается заглавной буквой над строчной буквой «а», как в - .
Чтобы нормализовать вектор a = [ a 1 , a 2 , a 3 ], разделите вектор на его длину || а ||. Так:
Базовый вектор
Единичный вектор, перпендикулярный друг другу. В двумерном пространстве вектор ( R 2 ) имеет два базовых вектора, а именно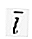 
= (1, 0) и 
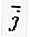= (0, 1).
Подобие двух векторов
Два вектора считаются одинаковыми, если они имеют одинаковую длину и направление.
Выравнивание двух векторов
Два вектора называются параллельными (параллельными), если линия, представляющая два вектора, параллельна.
Векторные операции
Скалярное умножение
Вектор можно умножить на скаляр, что также приведет к вектору, результирующий вектор будет:
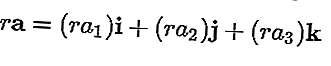
Сложение векторов и вычитание векторов
Например, векторы a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k
Результат плюс b: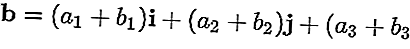 
векторное сокращение также применяется путем замены знака + на знак -
